Annotate chords and scales progression of MIDIs using MusicLang analysis
Abstract
Controlling the harmonic progression, which includes the chords and scales of a song, is an important ability in music generation tasks. The chords and the scales play a crucial role in defining a song's structure and emotional impact. In this article, we introduce a fast method for annotating the chord and scale progressions of MIDI files using our analysis package. We then show some use cases of this chord inference algorithm. All the code required to run the examples is available on GitHub.
Introduction : The chord scale notation
Discussing chord progressions often involves talking about the chords and the current scale. For instance, in the key of C major, the chords are C, Dm, Em, F, G, Am, Bdim. A simple progression like C Am Dm G can be represented as I vi ii V in the key of C major. The key points here include :
- the chord degree (I, vi, ii and V)
- the scale's root note : (C)
- the scale's mode : (major)
Additionally, one might consider two other musical characteristics of a chord :
- The chord inversion (examples include C/E, C/G, Dm/F, G/B, or as notated in figured bass roman numeral notation as I6, I64, ii6, V6)
- The chord extensions (such as C7, Dm(sus4), G13)
The figured bass notation can for example be found on diagrams like this :

Figure 1: Figured bass notation with roman numeral analysis. It is not to be mistaken with jazz chord annotation.
Automatically identifying a song's chord and scale progression would be extremely beneficial. However, this task is challenging due to several factors:
- Chords can vary in duration, requiring identification of potential chord changes.
- A single chord can correspond to multiple scales.
- It's necessary to distinguish between passing melody notes and chord notes in a way that mimics human perception of harmony.

Figure 2: What we want to achieve, labelling chord scale progression. But there are some difficulties, how to detect if a note is a chord note, and how to detect the chords starts on the first beat of each bar here ?
We propose some simplifications to tackle these challenges:
- Assume one chord per bar to simplify chord change detection. This approximation is useful, even though some bars may contain more than one chord, by highlighting the primary chord.
- Focus on two modes to limit the number of potential scales for each chord degree: major (in C: C D E F G A B) and harmonic minor (in C: C D Eb F G Ab B). These are the most commonly used modes in figured bass notation.
- Restrict the scale degrees to the first seven without alterations, diverging slightly from traditional roman numeral analysis. This restriction significantly reduces the potential scale options for each chord. For example, in C minor, the bVII (Bb major) would typically be considered, but here, it would be treated as the V of the relative major scale, Eb major.
Chord scale detection
Proposed algorithm
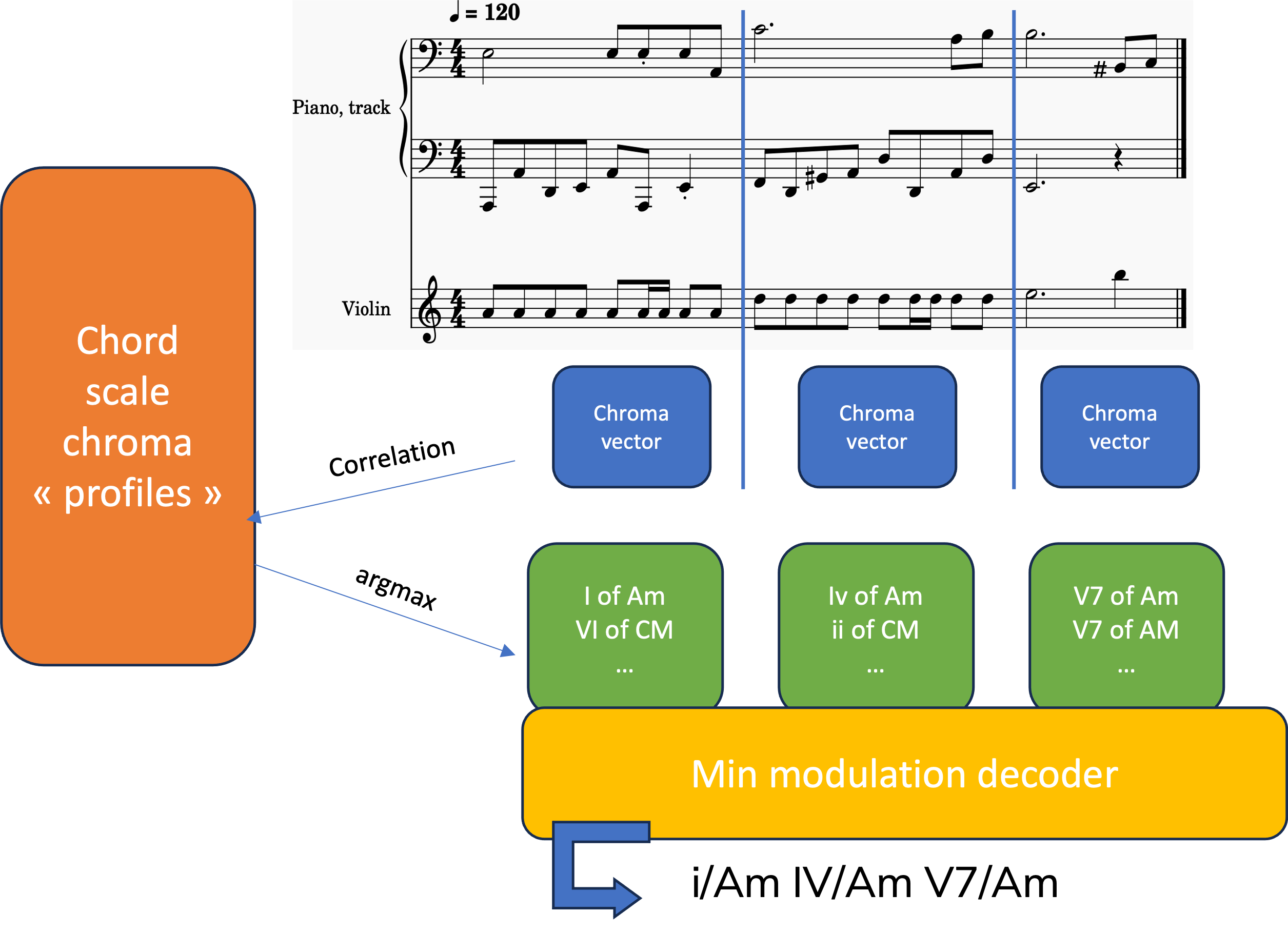
Figure 3: Proposed algorithm
We suggest a straightforward algorithm to identify a song's chord scale progression. The algorithm operates through these steps:
- Extract the chroma vectors for each bar: Instead of inputting raw notes into the algorithm, we extract the distribution of the notes (The number of C, Db, D, Eb, E, F, ... divided by the total number of notes) for each bar. This results in a 12-dimensional vector. Of course, we remove the drums beforehand.
- Query the most probable chord scale: With the chroma distribution of all bars in hand, we aim to identify the potential candidates for each bar, independent of the others. This is done by calculating the maximum correlation with a template database. Each chord (including root position extensions) and scale degree is linked to a chroma vector, which highlights the notes of the chord and scale to varying extents. Additionally, we apply a prior to each chord scale to assess its likelihood of appearing in a song. We then identify the chord scales with the highest correlation for each bar, adjusted by the prior. This process may yield one or more candidates depending on the chroma vector. For instance, if the chroma vector closely matches that of a C major in a C major scale, it might also be close to the chroma vector of C major in an F major scale, even equal if the bar lacks B or B flat notes. This method provides a solid estimate of the chord scale candidates.
- Extract maximum probability sequence: After identifying a list of candidate chord scales for each bar, our goal is to determine the most probable sequence of these chord scales. This is achieved by redefining our task as a Sequence Alignment or Edit Distance problem, which we solve using a straightforward dynamic programming algorithm. The key aspect we aim to minimize is the number of modulations, or scale changes, as naturally, sequences with fewer modulations, such as I/C major to ii/C major, are considered more probable than those like I/C major to i/D minor. We introduce a nuance in our edit distance calculation by not treating a change to a relative major or minor as a modulation, given their shared notes and common usage within the same piece. This approach allows us to formulate a clear problem that can be efficiently solved through dynamic programming, ultimately yielding a sequence of chord scales that minimizes modulations while aligning closely with chord scale templates.
- Find the inversion (the bass): Our analysis includes determining the bass note of each chord. To do this, we employ a simple algorithm that identifies the lowest note within the bar that is part of the chord and labels the chord's inversion based on this note. For example, if the lowest note is a G in a C major chord, the chord is labeled as C64 (second inversion).
Possible improvements
The proposed algorithm is fast and useful for many use cases. However, there are several possible improvements:
- Finetune the chord scale templates: The construction of the template chroma vector and the priors for each chord scale currently follow simple rules. A machine learning algorithm could be employed to refine these templates and priors using annotated examples.
- Improve the inversion detection: The algorithm may not always identify the lowest note as the actual bass note of a chord, as it could be a passing tone or part of an alternating bass pattern (a common example is alternating between the root note and the fifth below). A machine learning algorithm, enhanced with time information added to the chroma vector, could improve bass note detection using annotated examples.
- Improve vocabulary: Currently, the algorithm only considers triads and seventh chords built on the major and harmonic minor scales, along with sus2 and sus4 chords. Expanding the vocabulary to include more complex chords (e.g., ninth chords) and additional modes could offer more comprehensive analysis, though finding suitable templates for each new chord scale would be challenging.
- Detect chord changes: While the current approach assigns one chord scale per bar, it could be improved to detect chord changes at any point in the score. The Augmented Net, an open-source tool available here, addresses this challenge. Ultimately, the choice of algorithm depends on the specific use case; our algorithm offers robust and fast analysis, albeit with a limitation to one chord per bar.
Some code examples
All example comes can be run with our package available here.
Some basic usage of the package :
from musiclang import Score
score = Score.from_midi('data/bach_847.mid')
chords = score.to_romantext_chord_list()
print(chords)Output :
Here we have our chord progression, bar per bar of our midi file presented in the standard roman numeral notation. If you don't care about the scale you can also display the chords in the standard notation :
from musiclang import Score
score = Score.from_midi('data/bach_847.mid') # Your midi file here
chords = score.to_chord_repr()
print(chords)Output :
The chord progression is displayed on its simplest form : a sequence of chords. With musiclang you can convert it back to a chord/scale progression reusing the decoding algorithm we talked about earlier.
from musiclang import Score
chords_string ="DM A7 A7/C# GM"
chords_score = Score.from_chord_repr(chords_string)
chords = chords_score.to_romantext_chord_list()
print(chords)Output :
A bonus use case: Project a pattern onto a new chord progression
By parsing chord progressions in MusicLang, we're able to extract musical patterns that are independent of a song's specific chord progression. The example below demonstrates this capability by loading any MIDI file, extracting a pattern from the first bar, and applying it to a chosen chord progression. Additionally, we incorporate some counterpoint optimization to enhance the musicality of the example:
from musiclang import Score
from musiclang.library import *
from musiclang import Score
your_score = Score.from_midi("path_to_midi_file.mid")
# Chord projection on which we are gonna project our pattern
chords_string ="DM A7/C# GM/B A7 DM Cm Gm/Bb BbM DM/A AM DM"
chords_score = Score.from_chord_repr(chords_string)
# Assign duration to chords (here one chord will last 4 quarters)
chord_progression = chords_score.set_duration(4)
# Extract a pattern from the bach score
pattern = your_score[0].to_pattern(drop_drums=False)
score = Score.from_pattern(pattern, chord_progression)
score.to_midi('projection.mid')
score_arranged_with_counterpoint =score.get_counterpoint([score.get_bass_instrument()])
score_arranged_with_counterpoint.to_midi('projection_counterpoint.mid')
Let's here the original patterns and their variations on a given new chord progression :
| Chord progression | Original | Projection | Projection with counterpoint |
|---|---|---|---|
| DM A7/C# GM/B A7 DM Cm Gm/Bb BbM DM/A AM DM | |||
| Dm FM Dm/F Gm Dm/F FM Gm A7 |
Conclusion & Next steps
We've delved into a straightforward algorithm for identifying a song's chord scale progression and discussed its application using the MusicLang package. This approach unlocks many opportunities, such as extracting patterns from a song and projecting them onto a new chord progression. Moreover, it provides the means to create a chord progression generative model or a full music generator that can control the harmonic progression. In subsequent articles, we will explore the development of a tokenizer and a language model that build upon this.