The MusicLang tokenizer : Toward controllable symbolic music generation
Abstract
In this article, I introduce the encoding mechanism of musical scores when using the MusicLang model. I will detail the tokenization scheme and demonstrate its capacity to afford users profound control over the musical content generated by transformer models.
Introduction
The tokenization for symbolic music generation has been the subject of many investigation. A lot of research has predominantly concentrated on optimizing the performance of the next token prediction problem. Our research, at MusicLang, however, focuses on the controllability of the output sequence, a critical aspect for its application in music composition assistance. This facet of controllability has been less frequently addressed, possibly due to the challenge of quantifying an universal metric for controllability performance. In the novel tokenization scheme presented here, we employ an in-depth analysis of the musical score to distill pertinent musical information, which is then encoded within the tokenization process. Such comprehensive analysis enhances the capacity to finely tune the outputs of music language models trained using this approach. A side effect of the normalization used by this method is also to favour the learning of an efficient BPE compression, which is known to improve the performances of these models. Furthermore, we introduce a controlled generation framework designed to forecast music incorporating these control constraints. The methodologies for tokenization and prediction have been encapsulated in a fast-growing open-source initiative named musiclang_predict.
How to represent a score ?
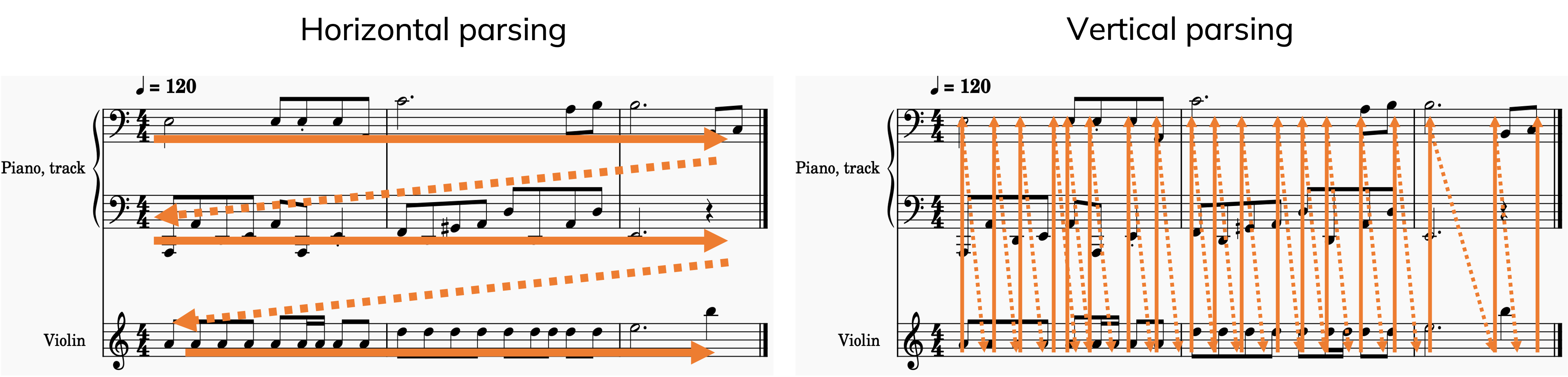
Figure 1: Horizontal VS Vertical parsing
When representing music with tokens, various parsing strategies can be employed, each presenting distinct advantages and disadvantages. A primary challenge is the simultaneous occurrence of musical events. Deciding the sequence in which to parse these events introduces a fundamental dilemma, a trade-off between melody or harmony representation. Below, we offer a comparison of these methods:
- Parse the music vertically, meaning notes are fully ordered timewise. It favours harmonically rich generation.
- Parse the music horizontally, meaning notes are grouped by voice. It favours melodic generation.
- Combine both methods: For instance, order notes by time within each measure, but overall, arrange them by musical part. There are many ways to do this.
Most tools designed for creating long music sequences opt for a mixed method. This reflects the way musicians typically read music:
- Measures act as key vertical breaks in music.
- Within a measure, instruments or voices are usually considered horizontally, yet in connection with each other.
- On paper, notes from the same instrument are often divided into distinct, meaningful parts.
It seems we generally interpret music in a combined manner, vertically within horizontal sections of a single measure.
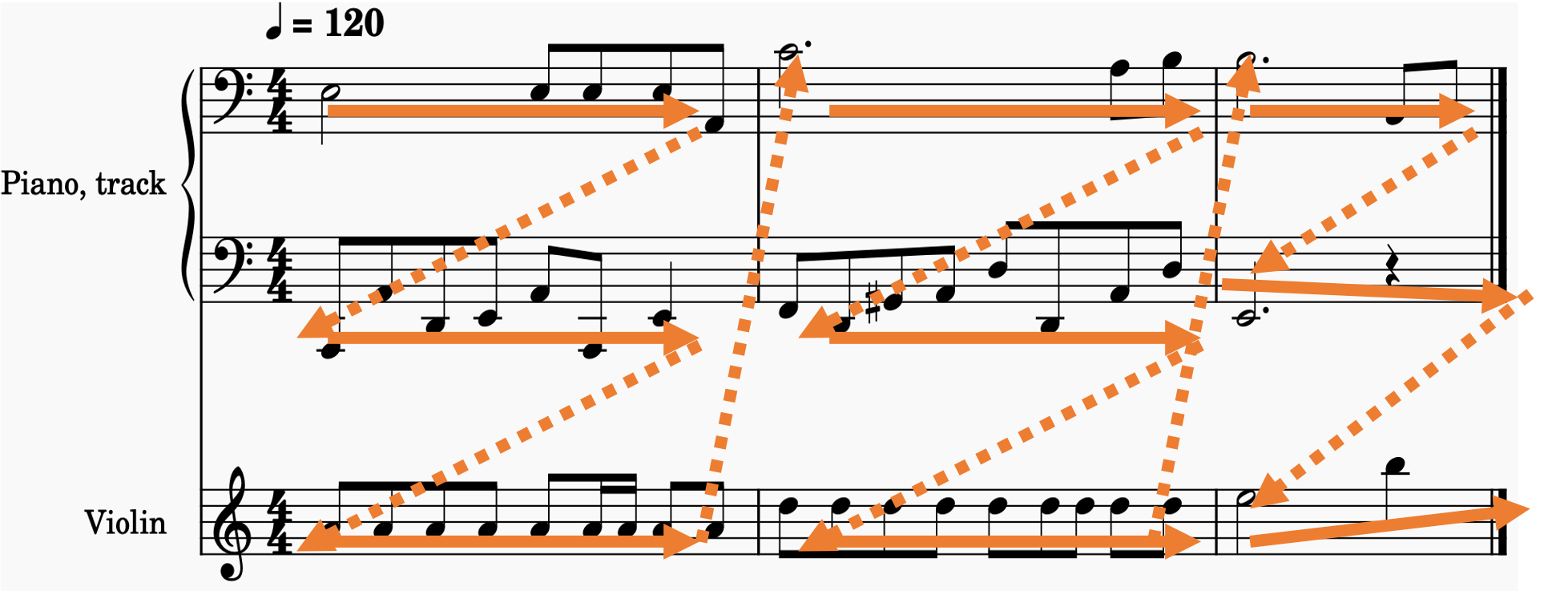
Figure 2: A natural way to process music
This "natural" approach to music representation guides the structure of our tokenizer: We depict music measure by measure. Within each measure, music is presented as a list of melodies, with each melody embodying a single-voice line from an instrument.
Tokenization overview
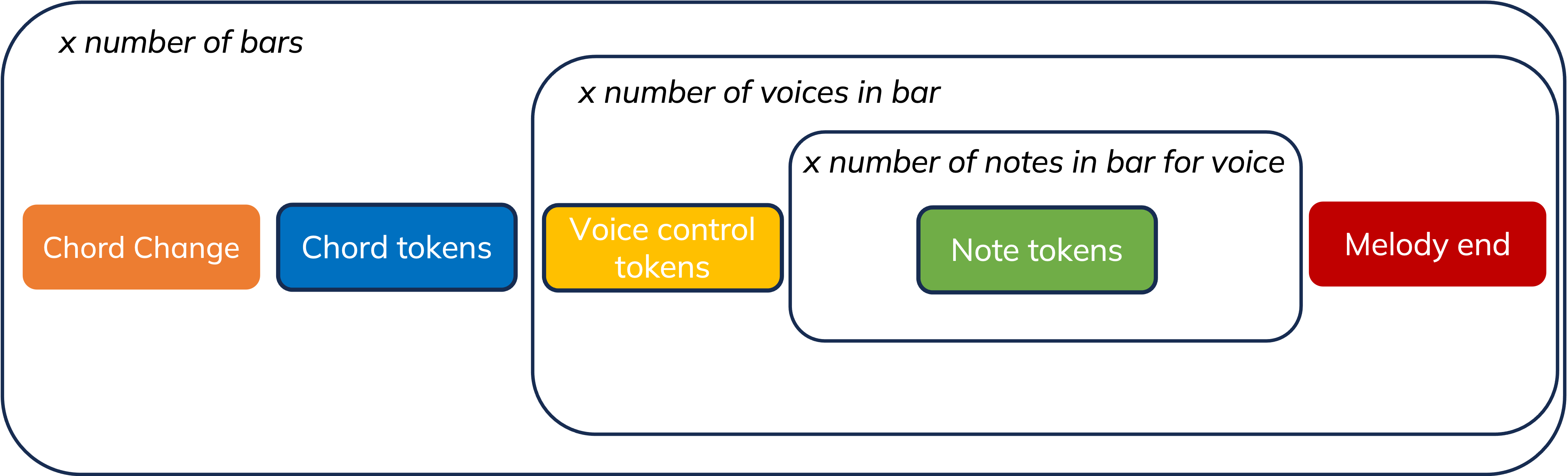
Figure 3: High level tokenization scheme
The tokenization scheme we propose consists of the following steps:
- Chord scale tokenization
- Melody control tokenization
- Melody tokenization
Let's delve into each module.
Chord scale tokenization
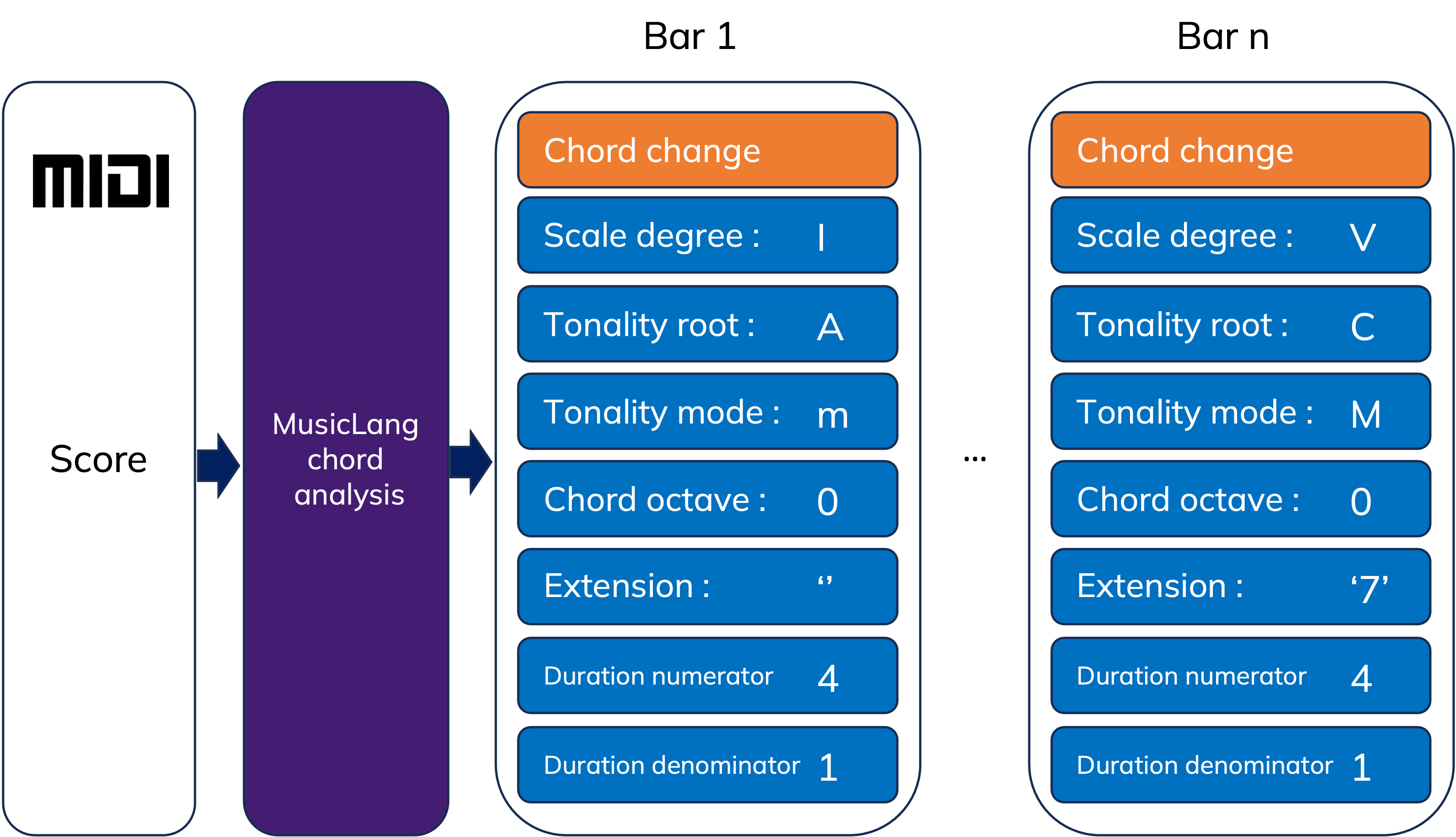
Figure 4: Chord scale tokenization scheme
Each chord is depicted using seven tokens (six control tokens plus one "CHORD_CHANGE" token):
- Scale degrees: I, II, III, IV, V, VI, VII - represent the chord's degree within the scale. This does not specify the chord's type; the mode and extension are needed for that.
- Tonality root: 0 to 12, corresponding to each pitch class possible (C to B).
- Tonality mode: m for harmonic minor, M for major.
- Chord octave: -4 to 4, indicating the root note's octave relative to the 4th octave.
- Extension: Uses figured bass notation to detail the chord's bass and any extensions (e.g., '' (triad in root position), '6', '64', '7', '65', '43', '2'), including variations with sus2 or sus4 for suspended chords.
- Duration numerator/denominator: Numerical values representing the chord's fractional duration, providing control over the time signature (since one chord equals one bar in MusicLang).
Please note that we are not only representing the current chord for each measure, but also the scale in which the chord belongs. It is very important because notes are also represented in the context of the current chord/scale root note. Finally we provide chord extension to be able to represent common figured bass notation. It will tell the model which notes are statistically more likely to be played in the context of the current chord and also what is the bass note of the chord.
Melody control tokenization
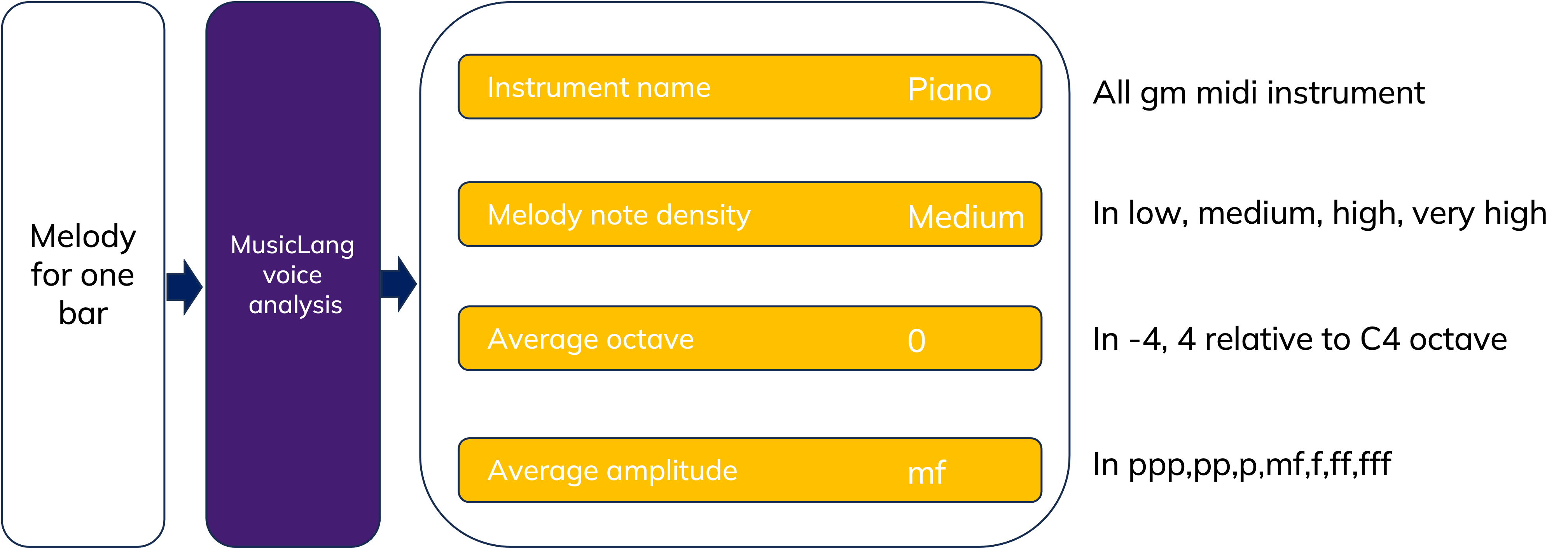
Figure 5: Melody (or voice) control scheme
In addition to control the chord progression and scale, we also provide a way to control the melody of each voice. This is done by providing a serie of token for each voice of each instrument, namely a note density (average number of notes per quarter) a note mean octave relative to the fourth octave, an average velocity in musical notation. Depending on the model version we also provide a token for voice index of the given instrument.
Note tokenization
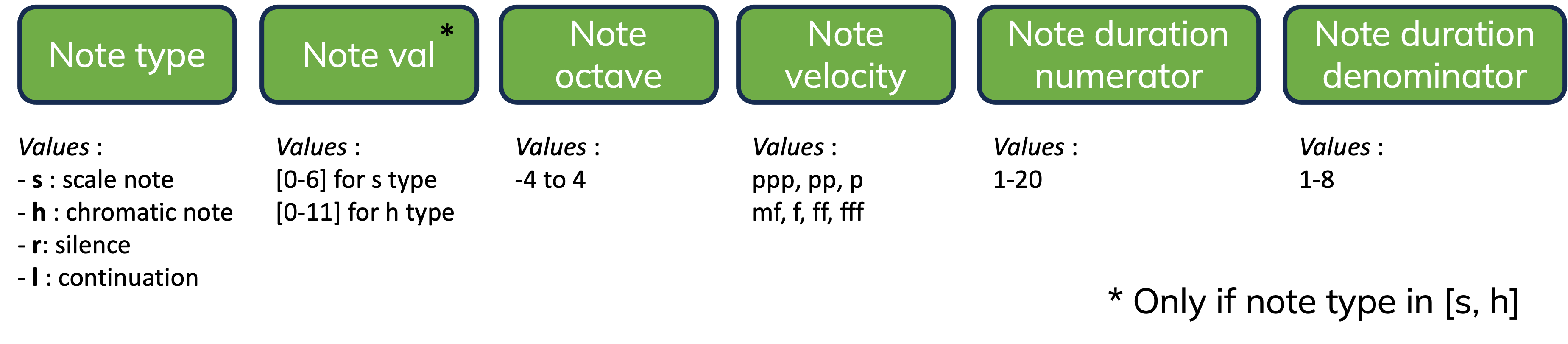
Figure 6: Note tokens
The scheme's primary innovation and inherent bias lies in its approach to pitch representation, which is relative to both the root note of a chord and a corresponding scale. For instance, in the context of a V chord in the key of C major (G major), the root note is denoted as s0. The second note in the chord's scale, A, is labeled as s1, and the sequence continues in this manner. Notes that are not part of the scale are marked with an 'h'. For example, h1 would represent an Ab in our V chord of C major. This method allows for a pitch to be understood in terms of its harmonic function and scale position. It gives to the model a direct "harmonic" values while generating melodies. This "normalized" representation is also very helpful to learn a BPE tokenization (Byte Pair encoding). Indeed many sequences of note tokens will look the same, independently of the tonality and mode of the song. That means that an encoding like BPE which is based on the frequency of sequences of tokens will be able to learn a lot more of common melodic patterns. We know that using BPE greatly improve the performances of language models, so we optimize it further by providing a normalized representation of the notes. I'll detail this in a future article.
Test the tokenization
Now, we implemented this tokenizer to be compatible with the HuggingFace API. With musiclang_predict you can easily test the tokenization on your own midi scores, and train your own model using this tokenization scheme. Here is a simple exemple of how to use the tokenizer to encode a midi file :
from musiclang_predict import MusicLangTokenizer from musiclang import Score # Load model and tokenizer, we use the v1 of the musiclang model for this purpose midi_file = 'path_to_your_midi_file.mid' score = Score.from_midi(midi_file) tokenizer = MusicLangTokenizer('musiclang/musiclang-4k') tokens = tokenizer.tokenize(score) print(tokens)
You will get a list of tokens formatted like this : ['CHORD_CHANGE', 'CHORD_DEGREE__4', 'TONALITY_DEGREE__5', 'TONALITY_MODE__M', 'CHORD_OCTAVE__-1', 'CHORD_EXTENSION__', 'CHORD_DURATION_NUM__4', 'CHORD_DURATION_DEN__1', 'INSTRUMENT_NAME__harpsichord', 'DENSITY__medium', 'AVERAGE_OCTAVE__0', 'AMPLITUDE__ff', 'NOTE_TYPE__r', 'NOTE_VAL__0', 'NOTE_OCTAVE__0', 'NOTE_AMP__mf', 'NOTE_DURATION_NUM__1', 'NOTE_DURATION_DEN__1', 'NOTE_TYPE__s', 'NOTE_VAL__4', 'NOTE_OCTAVE__0', 'NOTE_AMP__ff' ...
I also use the tokenizer do some other interesting MIR tasks like extracting a "song template" from a midi file. You input a midi file and get a json file containing all the control tokens of the song. Here is an example of how to do it :
from musiclang_predict import midi_file_to_template, predict_with_template, MusicLangTokenizer from musiclang import Score import json # Load model and tokenizer, we use the v1 of the musiclang model for this purpose midi_file = 'path_to_your_midi_file.mid' # For now this midi2template is independent of the tokenizer, it will only extract all possible control tokens from the midi file template = midi_file_to_template(midi_file) with open('template.json', 'w') as f: json.dump(template, f, indent=4)
The content of your file will look like this :
{
"tonality": "e",
"tempo": 130,
"time_signature": [
4,
4
],
"chords": [
{
"orchestration": [
{
"instrument_name": "acoustic_bass",
"instrument_voice": 0,
"amplitude": "mf",
"octave": 0,
"density": 0.5
},
{
"instrument_name": "drums_0",
"instrument_voice": 0,
"amplitude": "mf",
"octave": -2,
"density": 0.75
},
{
"instrument_name": "acoustic_guitar",
"instrument_voice": 0,
"amplitude": "mf",
"octave": 1,
"density": 0.5
},
{
"instrument_name": "acoustic_guitar",
"instrument_voice": 1,
"amplitude": "mf",
"octave": 1,
"density": 0.5
},
{
"instrument_name": "acoustic_guitar",
"instrument_voice": 2,
"amplitude": "mf",
"octave": 0,
"density": 0.5
}
],
"chord": "i64"
},
{
"orchestration": [
{
"instrument_name": "acoustic_bass",
"instrument_voice": 0,
"amplitude": "mf",
"octave": 0,
"density": 0.25
},
{
"instrument_name": "drums_0",
"instrument_voice": 0,
"amplitude": "mf",
"octave": -2,
"density": 1.0
},
{
"instrument_name": "acoustic_guitar",
"instrument_voice": 0,
"amplitude": "mf",
"octave": 1,
"density": 0.75
},
{
"instrument_name": "acoustic_guitar",
"instrument_voice": 1,
"amplitude": "mf",
"octave": 1,
"density": 0.75
},
{
"instrument_name": "acoustic_guitar",
"instrument_voice": 2,
"amplitude": "mf",
"octave": 0,
"density": 0.75
}
],
"chord": "i64"
}
]
}
This template is a nice summary of a song, defining its chord progression and outlining the melodic characteristics of each bars. From this base you can imagine a model trained to generate these template from a succinct prompt, and generating a full song from a template.
Conclusion & Next steps
Controllability is crucial for the practical application of music generated by music language models. I presented a tokenization scheme that allows users to manipulate various score parameters, such as chord and scale progressions, and even exert melodic influence over individual voices within each instrument. The effectiveness of this tokenization lies in the accuracy of the score analysis and the melodic normalization, introducing a significant inductive bias to the trained model, improving BPE tokenization and the overall model controllability. Next time we will be training a transformer model on this tokenization framework, and we will demonstrate the feasibility of generating music that adheres closely to a predefined prompt or song template. To experiment with these open-source models, please visit MusicLang Predict. Finally, this approach paves the way for a prompt-based music generation model. This could involve an intermediate model trained to produce the appropriate control tokens in response to a specified musical prompt.